Recent Posts
Recent Comments
Qaether 연구일지
[v1.0] 스피너구조 본문

- 스피너릿 (◇, \(\ell_s\)) - 잠재적 렙톤 루프
- 구성: 기본플라켓 ℓ₄ (F₁→Q₁→F₂→Q₂→F₁)를Q₁–Q₂ 축을 기준으로 90° 비평면 회전(플라켓 접기)
- 위상 폐합식(일반형) $$\sum_{(a\,b)\in\ell_s} \Delta\phi_{a b} \;=\; 2\pi\,n_{◇}, \quad n_{◇}\in\{\, -1,\,0,\,+1 \,\} = \Phi_{\rm loop} $$
- \(n_{◇}\)를 스피너릿 지수라 부른다.
- 전체 위상 홀로노미: 비평면 접힘(½)과 중성 보정을 합침$$\Phi_{\rm total} = \tfrac12\Phi_{\rm loop}+\pi(1-n _{◇} ^2) = \pi\,(- n_{◇}^2+n_{◇}+1)$$
- SU(2) 홀로노미:\[
S(2\pi)\colon
\Psi(n_{◇})\mapsto e^{i\Phi_{\rm total}}\,\Psi
=-\Psi
\quad(\forall\,n_{◇}\in\{-1,0,+1\}).
\] - \(n_{◇}\)별 입자 구분
- \(n_{◇}=+1:\;\text{양전자계열}\) - 어떤 위상차에도 0에 없는 구조
- \(n_{◇}=-1:\;\text{전자계열}\) - 어떤 위상차에도 0에 없는 구조
- \(n_{◇}=0:\;\text{중성미자계열}\) - 두 개의 위상차는 0, 두개의 위상차는 \(\pm\pi\)를 갖는 형태로 \(\pi\)는 \(-\pi\)와 같은 위상을 가지고 있어 사실상 구분이 불가하다. 따라서 0이라고 놓고 구분하기는 하지만 \(n_{◇}=\pm1\)의 형태도 가능.
- 스피너릿의 복합 입체 결합 예제 (잠재적 쿼크 루프)
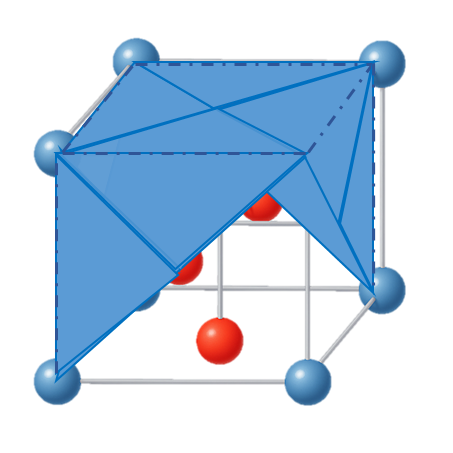
- 확장사면체

글루온 1개 + 스피너릿 3개 - 더블 확장사면체

확장사면체 2개 - Half Cover
- 확장사면체
'연구일지' 카테고리의 다른 글
| [v1.0] Pattern of 8 Gluon States (0) | 2025.06.15 |
|---|---|
| [v1.0] 결합 기준 입자 예제 (0) | 2025.06.14 |
| [v0.9] 동역학방정식 --> 위상경로적분 (1) | 2025.06.08 |
| [v0.9] 시간에 따른 위상의 변화가 인과율을 보존하는지 여부 (0) | 2025.06.07 |
| [v0.9] 격자 게이지 이론 유도 (0) | 2025.06.07 |


