Qaether 기본결합패턴 (루프) 정의 (v1.1)

결합패턴 정의

1. 기본루프
   • 트라이앵글릿 (Δ, \(\ell_3\))
     
     • 구성: 3개의 링크가 닫힌 형태.
     • 위상 폐합식:$$\Phi_{\ell_3}= \sum_{(ij)\in\ell_3} \Delta\phi_{ij} \;=\; 2\pi\,n_{Δ}, \quad n_{Δ}\in\{\,-1,\,0,\,+1\,\}$$
     • \(n_{Δ}\)를 트라이앵글릿 지수라 부른다.

       

       트라이앵글릿

   • 플라켓 (□, \(\ell_4\))
     • 구성: 4개의 링크가 닫힌 형태.
     • 위상 폐합식(일반형):$$\Phi_{\ell_4}= \sum_{(ij)\in\ell_4} \Delta\phi_{ij} \;=\; 2\pi\,n_{□}, \quad n_{□}\in\{\,-1,\,0,\,+1\,\}$$
     • \(n_{□}\)를 플라켓 지수라 부른다

       

       Plaquette

       
       
   • 스피너릿 (◇, \(\ell_s\))
     • 구성: ℓ₄ 플라켓(loop) 형태로 \(Q_1-Q_2\)를 기준으로 사각형 면이 90도 꺾임: $$F_1\xrightarrow{\ell_1}Q_1\xrightarrow{\ell_2}F_2\xrightarrow{\ell_3}Q_2\xrightarrow{\ell_4}F_1$$
     • 위상 폐합식(일반형): $$\Phi_{\ell_s}= \sum_{(ij)\in\ell_s} \Delta\phi_{ij} \;=\; 2\pi\,n_{◇}, \quad n_{◇}\in\{\, -1,\,0,\,+1 \,\} $$
     • \(n_{◇}\)를 스피너릿 지수라 부른다.

Spinnerlet

 

1세대 복합 입체 루프(잠재적 보손루프)

• 복합 입체 루프 구성을 위한 겉넓이 플럭스 보존
  • 플럭스 보존이란, 하나의 닫힌 입체(Polyhedron)를 구성하는 모든 면의 루프 지수 합이 0 이어야 한다는 뜻이다. 각 모서리(링크)의 위상차는 두 면 간에 공유되기 때문에, 모든 면 방정식을 더하면 내부 공유 링크들의 \(\Delta\phi\)항은 상쇄된다. 결과적으로 오직 외부 면(겉넓이)의 합만 남아야 위상적으로 결함(monopole)이 없는 상태가 된다.
• Tiara (정사면체)
  • 구성면: 4개의 트라이앵글릿 \(\ell_{3,1},\ell_{3,2},\ell_{3,3},\ell_{3,4}\)
  • 플럭스 보존:$$\sum_{k=1}^4 n_{\Delta_k} \;=\; 0, \quad n_{\Delta_k}\in\{\,-1,0,1\}$$
  • 예제: \((\,n_{Δ_1},n_{Δ_2},n_{Δ_3},n_{Δ_4}\,)=\{(1,1,-1,-1),(1,-1,0,0), (0,0,0,0)\}\)
  • 구현 불가: (1,1,1,1) 등 합 \(\neq0\) 조합.

    

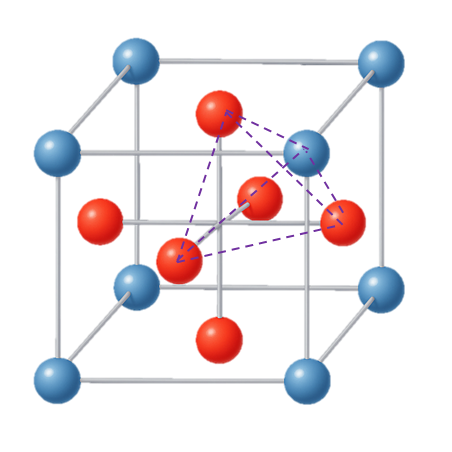
    Tiara

    
    
• Pyramid (정사각뿔)
  • 구성면: 4개의 트라이앵글릿 \(\ell_{3,1},\dots,\ell_{3,4}\) + 1개의 플라켓 \(\ell_{4}\) (밑면).
  • 플럭스 보존:$$\sum_{k=1}^4 n_{Δ_k} \;+\; 2\,n_{□} \;=\; 0, \quad n_{□}\in\{\,-1,0,1\}$$
  • 플라켓 \(n_{□}=\pm1\)일 때, 트라이앵글릿 합 \(\sum n_{Δ}=-2n_{□}\)
  • 해 예시 (스핀/색 발생용):$$\sum_{k=1}^4 n_{Δ_k}=-2$$ 예: \((n_{Δ_1},n_{Δ_2},n_{Δ_3},n_{Δ_4})=(-1,-1,0,0)\)
    • \(n_{□}=-1\) 일 때 \(\sum n_{Δ}=+2\) 예: (1,1,0,0)(1,1,0,0).
  • 해 예시 (평탄): \(n_{□}=0,\;\sum n_{Δ}=0\). 예: (1,-1,1,-1) 등.

    

    Pyramid

    
    
• Diamond (정팔면체)
  • 구성면: 8개의 트라이앵글릿 \(\ell_{3,1},\dots,\ell_{3,8}\)
  • 플럭스 보존:$$\sum_{k=1}^{8} n_{Δ_k} \;=\; 0.$$
  • 해 예시:
    • 4개 면 \(n_{Δ}=+1\), 4개 면 \(n_{Δ}=-1\) (합 0).
    • 모두 0인 면 8개 (완전 평탄)

Diamond

 

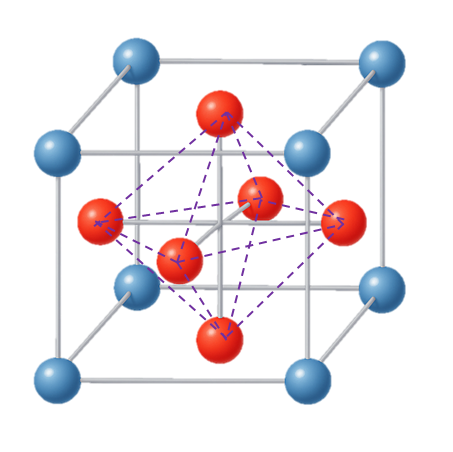
2세대 복합 입체 루프 (잠재적 쿼크루프)

이름	설명	구조
확장사면체	글루온(Y자형) 패턴 한개에 총 3개 스피너릿이 결합한 형태로 큐브의 1/4 덮개 구조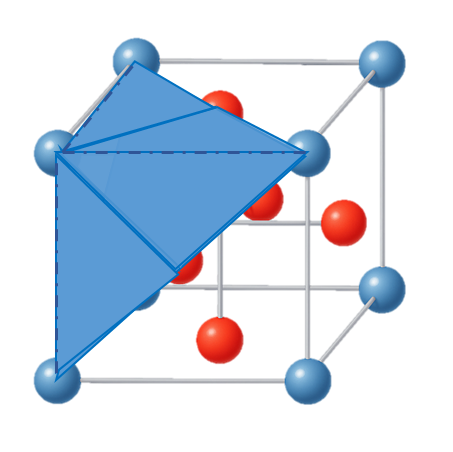
더블 확장사면체	2개의 확장사면체를 하나의 삼각면을 중심으로 접하게 하여 스피너릿의 4배 확장된 사면체로 만든 구조 (4배 확장 스피너릿이라고 불러도 좋을 듯)
확장팔면체	4개의 더블 확장사면체를 삼각형 면을 각각 접하게 하여 만든 구조
Half Cover	2개의 확장사면체를 선결합을 통해 큐브의 커버처럼 만든 구조
Full Cover	2개의 Half Cover를 가지고 만든 구조로 하나의 Half 커버를 180도 회전시켜 결합한 구조