[v0.6] 결합패턴 연구 in FCC structure

요즘은 FCC 격자 구조의 Qaether 모델을 그려놓고 결합 패턴에 대하여 이런 저런 고민을 해보고 있다.
이 그림으로는 어떻게 결합하는지 파악하기가 좀 힘들겠다 싶어서 아래와 같이 구의 크기를 줄여서 패턴을 파악해 보고자 한다.

그런데 이렇게 그려두면 공이 너무 많아서 복잡해 보여서 면에 박힌것과 꼭지점에 박힌것을 구분해보자.

격자 안에서 일단 안정적인 결합을 한다고 했을때 어떤 결합이 가능할지부터 시작해보고 싶었다.
이런 저런 결합을 시도해보면서 알게 된 내용은 폐곡선으로 닫힌 결합의 경우 위상차의 합이 반드시 2π가 되어야 한다는 것이다. 그렇지 않을 경우 결이 맞지 않아서 안정적인 결합을 이룰 수가 없고 그 위상차에 의해 구조 붕괴를 일으킬 수 있다.
일단 폐곡선으로 닫히는 2차원 평면 결합을 우선적으로 찾았더니 정삼각형, 정사각형의 3가지 형태로 나타났다.
첫번째, 삼각형은 면 중심을 잇는 삼각형 하나와 면중심 두개에 꼭지점 하나를 잇는 형태가 가능하다. 꼭지점 두개에 면 하나의 경우는 꼭지점 두개가 직접 결합 불가이기 때문에 불가하다. 그런데 이 경우 모두 정삼각형을 이룬다. 면 중심을 잇는 삼각형 패턴은 총 8개가 나오고 꼭지점과 두개의 면 중심을 잇는 삼각형은 꼭지점별 3개씩 총 24개가 나온다. 따라서 평면 정삼각형 결합은 총 32개가 나온다.
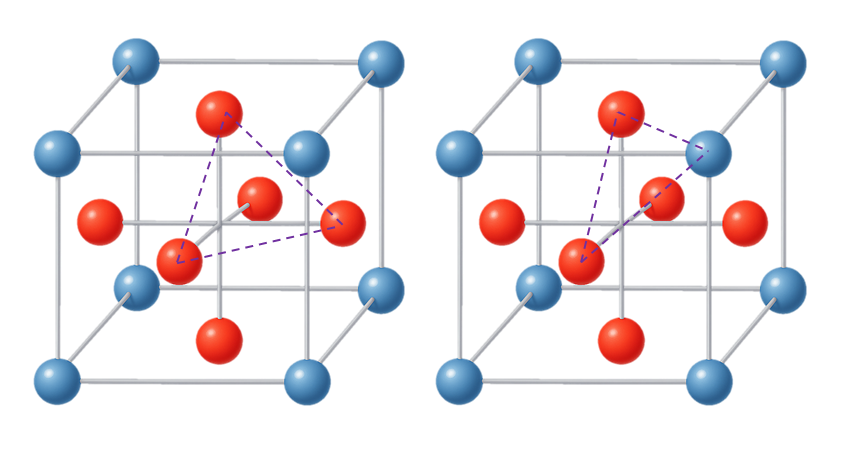
다음으로는 이 삼각형을 가지고 만들 수 있는 다면체에 대하여 알아보자.
꼭지점을 하나를 중심으로는 닿아있는 세개의 면 중심과 다른 면들의 중심을 하나씩 결합하여 총 세개 삼각형이 만들어지고 이 삼각형 4개를 합해서 하나의 정사면체 결합도 생성된다. 정사면체 결합은 꼭지점 별로 하나씩 생기며 총 8개가 생길수 있다.

두번째 사각형은 면 중심을 잇는 정사각형 하나 그리고 면중심에서 꼭지점과 연결하는 정사각형 하나가 생긴다. 면중심을 잇는 정사각형 결합은 3개가 발생하며, 두개의 격자를 연결하여 만들 수 있는 정사각형 결합은 6개 면중심 기준으로 4개씩 생기지만 1/2만 지분이 있으므로 사실 12개가 생긴다. 따라서 모든 사각형의 숫자는 전체 15개가 발생한다.

최근접 결합에 의한 사각형 결합은 이 2개를 제외하고는 없다. 삼각형과는 다르게 이 사각형만을 이용해서 만들 수 있는 최근접 결합 육면체는 없다. 삼각형과 결합을 하면 다음과 같은 다면체들을 만들 수 있다.
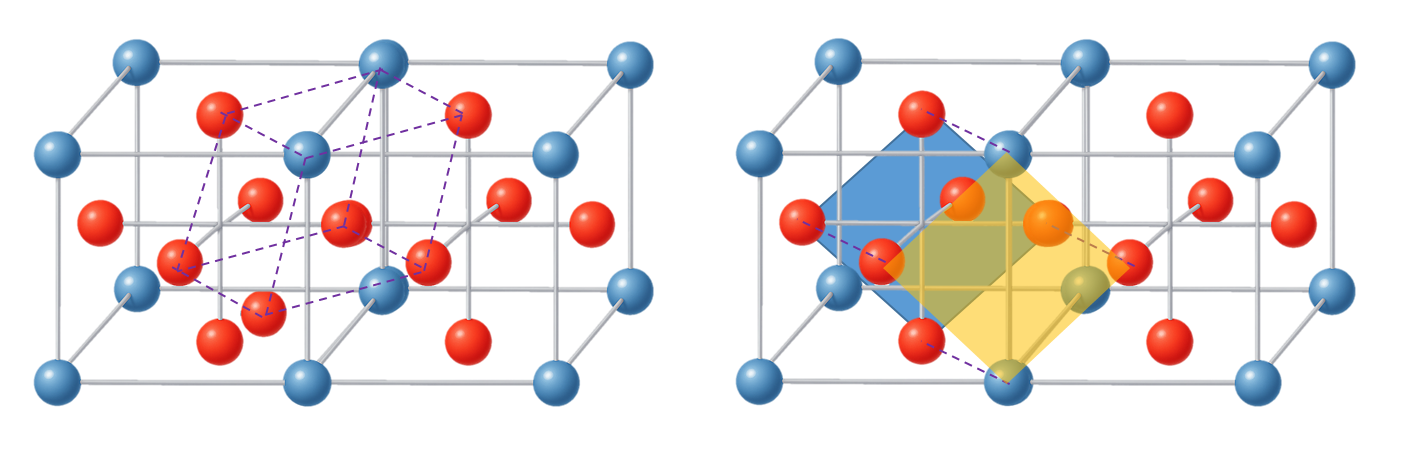
첫번째 패턴은 정팔면체 패턴으로 삼각형 8개를 이용하여 중심 Void를 정팔면체 형태로 감싸는 구조이다. 딱 1개 존재한다. 재미있는 부분은 삼각형 8개로 만들어진 것처럼 보이기도 하지만 사각형 패턴 3개로 만들어지기도 한 구조라는 점이다.

두번째 패턴은 두개의 큐브를 결합하는 경우 그 사이에 사각형을 형성하고 그 사각형에 수직으로 최근접하는 면중심 공과 연결하는 피라미드 패턴이 가능하다. 이 패턴은 면 하나당 4개가 발생하고 총 6면이므로 24개가 생기지만 1/2 지분을 갖기 때문에 총 12개가 발생한다.
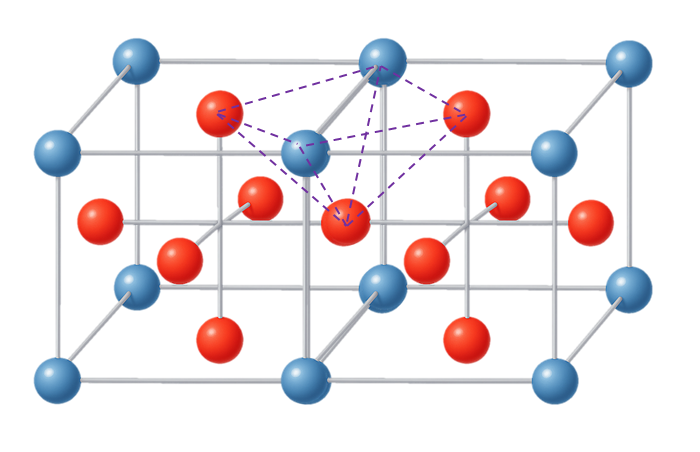
다음 패턴은 간단히 설명하면 사각형 두개를 붙이고 각 테두리선을 기준으로 90도, 270도 꺾은 도형이다. 이를 좀더 자세히 설명하면 면중심에 있는 공을 F라고 하고 테두리에 있는 공을 Q라고 했을때 \(F_1-Q_1-F_2-Q_2-F_1-Q_3-F_3-Q_4-F_1\) 과 같은 사각형 두개를 연결한 도형을 만들고 \(Q_1-Q_2\)와 \(Q_3-Q_4\) 선분으로 각각 90도와 270도 꺾으면 된다. 이런 패턴은 한 면에 4개씩 생기는데 육면체 이므로 24개가 생기고 다른 큐브들과 1/2씩 지분이 나뉘므로 총 12개가 생긴다.
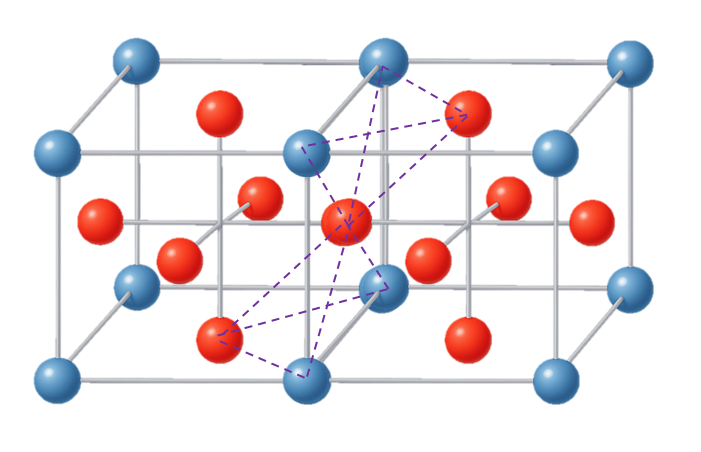
그런데 위 피라미드 결합과 스피너 결합은 재미있는 특징이 있다. 스피너 결합의 경우 완벽한 입체가 아니어서 void를 감싸지 않는 구조이지만 스피너의 한쪽을 거울대칭 시키면 피라미드 결합이 되면서 void를 감싸게 되는 구조로 바뀐다.
이것들을 기반으로 Qaether의 기초 결합패턴을 정리해보면 삼각결합 2종류 패턴, 사각결합 2종류 패턴, 정사면체 결합 패턴, 정팔면체 결합 패턴, 피라미드 결합, 그리고 스피너 결합이 있다.
이런 기초 결합패턴들을 가지고 다양한 패턴을 만들어 갈 수 있는데 조금은 의미있는 결합 형태는 다음과 같다.
스피너에 정사면체를 결합한 형태인데 기존 스피너의 대칭성이 유효한 구조로 스피너의 각 면4개에 최대 4개의 정사면체를 붙일 수 있다.

다음으로는 피라미드 결합구조에 정사면체를 붙이는 구조로 역시 4방향으로 정사면체와 결합이 가능하다.
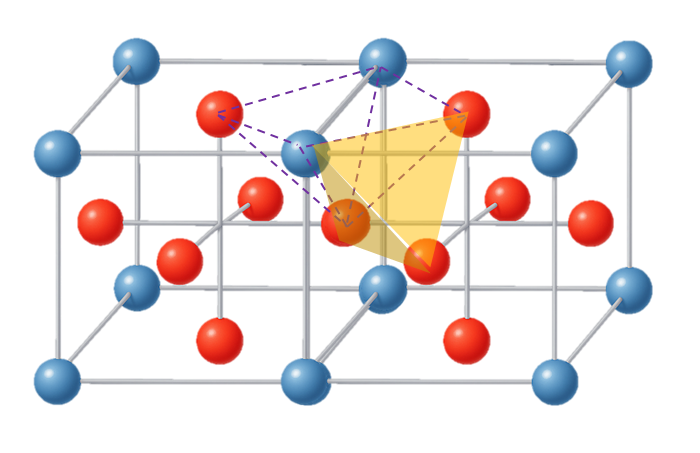
이런 결합이외에도 다양한 패턴을 정삼각형, 정사각형, 정사면체, 스피너, 피라미드, 정팔면체등을 결합하여 만들어 낼 수 있다.
마지막으로 정팔면체 패턴에는 정사면체가 면결합하기가 아주 수월하다. 그리고 그렇게 결합하고 나면 자연스럽게 피라미드 결합구조가 다음 큐브사이에서 발생한다.